History is not so linear as it tends to be seen from the present. The development
of the modern energy principle was not achieved on a direct path without
detours. I'm no follower of the whig interpretation of history, where
every detail is a logical consequence of previous details.
Here, I've conciously made the connection between persons far apart in time.
Persons which at the first glance are not directly connected. Sometimes the
development of ideas was in parallel. After a long history starting from
ancient times, a first systematic approach to phenomens like gravity was
made in the 17th century. Nevertheless, it still took 200 years until
Joule could prove the equivalence of heat and mechanical power formally and
by experiment.
When reading this chapter, you may come to the conclusion that I'm member
of the so-called establishment1).
The Beginnings
Which ideas were vivid before perpetual concepts came up? If we look far
into the past, only a few sources are available. One particular greek philosopher
is worth mentioning in this context. Around 500 B.C., Anaxagoras stated
"nothing can be generated out of nothing and nothing can be annihilated."
(cf. Michal p.113). Later this
principle was frequently cited as ex nihilo nihil. From today's view
it is difficult to decide, if this postulate imposed delay to the development
of the perpetual motion idea.
 |
|
Aristotle (384 B.C. - 322 B.C.) was a huge milestone. With him science
was condemned to bad fortune for a long time. Aristotle not only developed
the aristotelian logic, but also made these statements, which nobody dared
to check:
-
Heavy bodies fall faster than light bodies.
-
Light bodies raise.
-
A moving body needs the surrounding air to be in movement. The air opens
in front of the body and closes behind it, thus pushing it forward. The idea
of the horror vacuui was born. With this, also the distincion beween
perfect, celestial movement and terrestrial, forced movement was founded.
-
With aristotelian logic he proved the inferiority of women.
-
Migrant birds vanish because they dig themselves into the swamps.
-
Bent things cannot be measured with straight lines. With this, the principle
which today is associated with Cavalieri's name, but in fact was found and
used by Archimedes, was doomed to Hades for almost two millenia.
|
Today's world may look different, if Aristotle had refrained himself to being
philosopher instead of doing physics and math. Nobody had the courage to
challenge Aristotle's authority. Experiments were regarded as unneccessary,
although he did not write disrespective of it. Aristotle's epigones were
much worse than the master. We have to keep in mind, that at Aristotle's
time, other theories were discussed as well, e.g. Demokrit's postulate of
atoms. The hayday of ignorance were the late middle ages, when the scholastic
Thomas Aquino entered the stage who was the most brilliant aristotelian follower
at his time.
Thomas Aquino
 |
|
Thomas Aquino (1125-7 Mar. 1274) was a representative of the meanwhile
completely cemented aristotelian curriculum. By use of the aristotelian logic
and scholastic trickery he proved the infallability of the pope, who then,
by the authority of his infallability, declared Thomas Aquino's curriculum
for correct. Especially the aristotelian opinion now became dogma. By this,
it should take additional 400 years, until modern ideas could develop.
Consequently, the development of science was delayed by almost 2000 years.
This gave an ideal basis for alchemists and perpetual motion seekers, whereas
serious researchers like Copernicus, Galilei and others suffered under the
dogma and many researchers even had to pay with their lives. |
Leonardo da Vinci, Engineer and
Universal Genius
 |
|
Leonardo da Vinci (15 April 1452 - 2 May 1519) had a life-long interest
in perpetual motion machines. It is very difficult to write about Leonardo
without emotions and the use of superlatives. There seems no region of science,
art and technology that has not been covered by Leonardo. He is a monolith
without comparison and even later scientific geniuses like A. Kircher lack
many aspects of his universality and ingenuity. To us, his remarks on
recirculation mills and the proof of the impossibilty of mechanical perpetual
motion are of particular interest. He stated: "Oh you researchers of perpetual
motion, how many harebrained ideas have you created in this search. You may
as well join the gold-makers." With that, and other remarks about the
conservation of work in water machines, he came quite close to the first
law of thermodynamics.
|
 |
|
The mathematician and researcher of nature Simon Stevin (1548-1620) worked
around 1586 (i.e. 130 years before Bessler's fraud) on the perpetual
motion topic. Stevin wrote a book entitled De beghinselen des
waterwichts in which he discusssed the impossibility of perpetual motion.
He took a chain loop on ramps of different steepness as a starting point
to develop his proof. Although Stevin's arguments may not be challenged to
today's rigorous formal criteria, his proof was a great step forward in physics.
|
Johannes Kepler
 |
|
Johannes Kepler (27 Dec. 1571-15 Nov. 1630) was astronomer and Tycho
de Brahe's assistant. Later he followed Brahe in the postion as astronomer
royal at imperator Rudolf's II court in Prague. Kepler was follower of the
Copernican heliocentric thesis. Based on the excellent observation material
which his teacher and predecessor had left to him, he could systematically
work on the mathematical theory of the planets' paths. It took a while until
Kepler gave up the circular paths in favor of elliptic trajectories. By
tremendous effort, Kepler calculated his results and after 20 years of hard
work, he did not only present his now famous laws to the public, but also
very precise astronomic tables which were widely known as the "Rudolphinic
tables", which were a great milestone in the history of astronomy.
Kepler was able to describe how the planets move round the sun, but
why they do it in exactly that way, he either
could not describe or was unwilling to do2). |
Galileo Galilei
 |
|
Galileo Galilei (15 Feb. 1564 - 8 Jan. 1642) introduced the combination
of experiment, measurements and mathematical theory as scientific method.
By this, he openly opposed the predominant opinion that Aristotle had already
said everthing and it is sufficient to teach his writings. Galileo especially
made research in mechanics topics e.g. the fall of bodies. He proved by theory
and experiment that Aristotle was wrong. In some aspects, Galileo remained
in the traditional aristotelian science, as he was a follower of the horror
vacui theory although his pupil Torricelli proved by experiment the existence
of the air pressure. |
John Wilkins
 |
|
Bishop John Wilkins (1614-1672) was a co-founder of the Royal Society.
His famous book Mathematical Magick was extremely important for the
history of science in general and the history of perpetual motion in particular.
His introduction to the chapter "Dædalus" which covers the science
and technology of PMMs even today is worth reading, like all other passages
of his book as well: "This is the great secret in Art, which like
the Philosophers Stone in Nature, hath been the business and study
of many more refined Wits, for divers ages togethers; and it may well be
questioned, wheter either of them as yet, hath ever been found out, though
if this have, yet like the other, it is not plainly treated by any Author.
Not but there are sundry discourses concerning this subject, but they are
rather conjectures than experiments. And though many inventions
in this kind, may at first view bear a great shew of probability, yet they
will fail, being brought to trial, and will not answer in practice what they
promised in speculation. Any one who has been versed in these experiments
must needs acknowledge that he hath been often deceived in his strongest
confidence; when the imagination hath contrived the whole frame of such an
instrument, and conceives that the event must fallibly answer its hopes;
yet then does it strangely deceive in the proof, and discoversto us seme
defect, which we did not before take notice of." (Mathematical Magick, pp.
224-225)
Except Leonardo, nobody before had so clearly denied the possibility of man-made
perpetual motion. |
Christian Huygens
 |
|
Christian Huygens (14 Apr. 1629-8 June 1695) made detailled research
in mechanics of rotating masses. He developed the theory of rotational momentum
and conservation of impulse. Huygens described the dependecy of centripetal
force from mass, radius and angular velocity. With this, a good foundation
for Newton was prepared. |
René Descartes
 |
|
René Descartes (31 Mar. 1596-11 Feb. 1650), named
Cartesius, stated that the "overall sum of all products of
quantitas materiae and velocity in the world is constant."
Cf. Michal, p. 85. Although Descartes
came closer to the principle of conservation of energy, his opinion about
force caused great confusion and quarreling between scholars. Obviously,
nobody made the effort to experimentally verify Descartes' opinion or check
its plausibilty formally. As indirect theoretical consequence, the door was
open for inventors of perpetual motion machines. It needed some more time,
until Leibniz and Newton clarified the differences between force, work, impulse
and energy. |
Isaac Newton
 |
|
Isaac Newton (4 Jan. 1643-31 Mar.1727) brought light into the whole planet
movement confusion. The legend says, Newton leaned at an apple tree, as an
apple fell onto his head. This caused a historical impulse! "Why does the
apple fall? Why does the moon not fall? Of course the moon would fall,
but this is compensated by the centripetal force caused by its rotation around
the earth.
Newton's gravitational law was the preconditon needed to make Kepler's laws
concludent. Besides this, the much more important result was the understanding
of force and potential energy. Leibniz, Newton's rival,
had already come to comparable results. |
Gottfried Wilhelm Leibniz
 |
|
Gottfried Wilhelm Leibniz (1 July 1646-14 Nov.
1716) did not accept Descartes' theory. He argued: "If a mass of 1 pound
falls 4 yard, it gains such »force« that allows to move it up again
to the same height. If a mass of 4 pound drops by 1 yard, it gains a
»force« to lift it again to 1 yard. 1 pound lifting 4 yard must
be the same as lifting 4 pounds for 1 yard
[...]"3)
(Michal p.86). This approach led to
a massive scholarly quarrel between Leibnitz' and Descartes' followers. It
took a while until force and work were cleanly defined and sorted. Scholars
like s' Gravesande made bad experiences in this process. |
 |
|
's Gravesande (27 Sep. 1688-28 Feb. 1742) was one of the scientists
who was honestly convinced that the construction of a perpetual motion machine
is possible. He lived at the hayday of the PMM delusion.
What were the reasons? Mechanical arts and skills were, compared to previous
centuries, far more developed. Engineers like Ramelli or Leupold published
large volumes which systematically collected machine descriptions. Although
some of these constructions seem to be of less practical value from today's
point of view, there seemed to be only a few mechanical tasks that could
not be solved.
One of the reasons for the opinion that a PMM is possible was Descartes'
theory that a falling body wins force on its way. From our point of
understanding, this is a confusion of force and impulse. But under the assumption
that Descartes was right, it could be proved that a PMM was possible.
s' Gravesande followed this opinion, until he learned of Newton's
gravitational law. Newton could also show that Descartes' theory of force
was based on a misunderstanding.
s' Gravesande was one of the first scholars on the continent who actively
engaged himself in making Newton's theory popular. |
The theory of gravitation proved to be a very powerful concept. Unfortunately,
's Gravesande had examined Bessler's
machine and already written a positive scientific essay. As the fraud
was uncovered, 's Gravesande escaped into flimsy excuses. In fact, he
was no more convinced of the creation of perpetual motion by human hands.
Let's say, in the mechanical area. As far as (Al)chemy was concerned, he
still expected unknown possibilities to reach that aim.
Academic Statement
The French academy of sciences published in their 1775 annals a statement
starting with the sentence: "La construction d'un mouvement perpétuel
est absolument impossible".
Klemm (p.18) and
Michal (p.110). A translation of the
most important text passage: "It is impossible to obtain perpetual motion.
Even if in long terms friction and resistance of the medium would not destroy
the result of the moving force, this force could only cause a reaction that
is equal to the action." That was the decided final blow for the perpetual
motion concept, although this blow was made on somewhat instable feet. Until
the final formulation of the energy principle, 100 more years needed to pass.
The physics section gives a full account and translation of this historical
document.
Around 1840, the time for the discovery of the principle of conservation
of energy had come. Thus, Mayer, Helmholtz and Joule laid the foundation
of the theory at almost the same time. Finally the denying opinion of the
French academy of sciences got its late justification.
Julius Robert Mayer
 |
|
The german physician Julius Robert Mayer (25 Nov. 1814-20 Mar.1878) wrote
in 1841 a treatise which was published 1842 in Liebigs Annalen der
Chemie (Liebig's chemical annals): Bemerkungen über die Kräfte
der unbelebten Natur. (Remarks about the forces in the non-living nature).
The treatise describes the calometric research Mayer made during his work
on the consumption of food of living beings. The medical scientific world
only had a friendly look at Mayer's text. But after first hesitation, it
caused a revolution in physics.
Mayer calculated the mechanical thermal equivalent, but not those for other
forms of energy. The apparatus Mayer used can be seen in the Deutsches Museum
in Munich. With his method, Mayer came quite close to the value which is
today accepted. |
Hermann Helmholtz
 |
|
Like Mayer, Hermann Helmholtz (31 Aug. 1821-8 Sep. 1894) was physician.
1848 he published a treatise in which he formulated the principle which today
is called "principle of conservation of energy".
"Inside a closed system, i.e. a system into which neither energy is transported
nor taken out of it, in which arbitrary processses (mechanical, thermal,
electrical, chemical) happen, the total energy remains
conserved"4)
(Kuhn, Physik IIIB, S.108)
|
James Prescott Joule
 |
|
1843, James Prescott Joule (24 Dec. 1818-11 Oct.1889) experimentally
determined the mechanic equivalent or thermal energy. Moreover, he found
out which amount of mechanical work is necessary to generate a particular
amount of electric energy. He also found a conversion factor between electric
and thermal energy. Joule clearly found out that different forms of energy
could be transformed into each other and what the conversion factors were.
Today, to Joule's honour, the energy unit is named "1 Joule", independent
from the type of energy. |
Ludwig Boltzmann
 |
|
Ludwig Boltzmann (20 Feb. 1844 - 5 Sep. 1906) worked on the foundation
laid by Mayer, Helmholtz and Joule. Boltzmann drew his conclusions of the
already discovered Brownian molecular motion. The discovery that temperature
is equivalent to motion and that thermodynamical phenomena could be described
by statistical methods were a great step forward to an uniform energy principle. |
James Clerk Maxwell
 |
|
Maxwell (13 June 1831 -5 Nov. 1879) is widely known for his famous equations.
But Maxwell did not only work in the area of magnetism and electrodynamics,
but also made research in the field of thermodynamics. Here he laid a solid
theoretical foundation based on refined mathematical methods. Maxwell is
the inventor of the famous Gedankenexperiment to construct a PMM of the second
kind; a PMM which does not contradict the law of energy conservation. Known
as Maxwellian Demon, it became part of the history
of modern science. |
Rudolf Clausius
 |
|
The modern definitions of the laws of thermodynamics were formulated
by Rudolf Clausius (2 Jan. 1822 -24 Aug. 1888):
-
In a closed system, in which arbitrary mechanical and thermal processes
happen, the total energy is constant.
-
The energy of the universe is constant. The entropy of the universe
increases to its maximum.
Clausius' work is a milestone touching the borders of classical mechanics.
Differences between theory and practice, which were already found by experiments
around 1900, could not be explained by classical theory any more. It needed
Einstein's, Planck's and Heisenberg's results to explain these mismatches.
Walter Nernst (25 June 1864-18 Nov. 1941) added a third law of
thermodynamics:
The entropy of condensed systems reaches at sufficiently low temperatures
a constant value. |
Max Planck
 |
|
As a byproduct of his quantum theory, Max Planck (23 Apr. 1858 - 4 Oct.
1947) could explain why the Maxwellian Demon must remain a Gedankenexperiment
forever. Moreover, Planck could restrict the third law of thermodynamics
to:
At a temperature of absolute zero, the entropy of uniform condensed
systems is exactly zero. |
Patents
Since many years, patent offices do no more accept patent applications for
perpetual motion machines5). This is
an obstacle for inventors who want to get their PMM patented. Frequently
they use the trick to describe their machines in a way that causes no suspicion
or they simply declare it as something else.
Michal gives a pretty example of such
a device and cites from the patent application:"...in the lower part of the
machine stand, there is a manually operated brake, to prevent the machine
to reach a state of permanent
motion"6) (p. 112-112). At least the
inventor was clever enough to face Prof.
Bürger's PMM consideration with a suitable countermeasure.
Like many others the abovementioned inventor may have been convinced from
his idea. But other inventors hat fraud in mind, either of greedyness for
money, of need of publicity or to surprise the spectators.
And then there are others, which fall viction of the great conspiration of
the scientific establishment. A typical example is Mr.
Bourbaki (as
far as I know not a relative of the mathematician
Bourbaki7)
Those who want to learn a little more about patent-related topics of perpetual
motion machines and some interesting designs should have a look at the site
Perpetuum Mobile of the german patent office (Deutsches
Patent- und Markenamt).
The first law does not disallow this nice "machine":
| |
Take a box filled with gas and divide it with a separating wall in two
chambers. Now in both chambers is gas with the same pressure and temperature.
That means that both chambers contain a mixture of molecules of different
speed. In the middle of the separator is a tiny whole, that allows passing
of a single gas molecule. The hole can be shut by a flap. A very quick
demon (the Maxwellian!) who has very sharp eyes observes the gas molecules
and opens the flap every time when a quick molecule in the left chamber
approaches the hole. As the flap is open, the molecule can pass to
the right chamber. Slow molecules from the right chamber will be allowed
to pass into the left chamber. All other molecules must remain in their current
chamber.
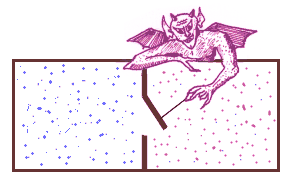
As time goes by, in the left chamber all slow molecules will be collected
whereas in the right chamber all quick molecules can be found. In other words:
The left chamber cools down, the right chamber heats up. By the temperature
difference of these two chambers, a heat engine can be powered. After passing
through the engine, the waste gas mixture can be fed back into the two chambers
to keep the demon busy. The whole setup is known as a perpetual motion
machine of the second kind. |
As the first law does not forbid to build this machine, there are always
inventors who try to refurbish the idea again. They know that the second
law is based on statistics, thus maybe containing a loophole. The latest
project I've heard of was Sanjay Amin's
entropy engine.
Application of Theory
As the theory and its history briefly described here seem not to have settled
in some inventors' minds, I have collected some typical conceptual flaws
and how to explain them. My
physics chapter gives
an introduction to disappoint geniuses.
Remarks:
1.
Establishment
is the name which perpetuum mobile inventors, flat-earth promotors and other
"researchers" use for the established science, which does nothing else than
critically ask about those things that are claimed or seem to be really
are. These established methods mostly are simple, but effective
and normally consist of a mixture of obvious knowledge and mathematical methods.
Of course, this makes the establishment suspicious to be the source of the
great conspiration which targets at disqualifying the real
geniouses and their ideas.
2. About
Kepler I feel the need to make a few remarks.
Why had that excellent mathematician not found the physical law, which today
is called "gravitational law"? Why did Kepler regard his famous laws about
the motion of planets as a not so important result? Why did the rational
thinker work as a court's astrologist, apparently convinced of the methods
he used? What motivated Kepler to write his large opus "Harmonices
Mundi"?
Now we have reached our own horizon! Today's way of thinking is dominated
by using causal or cuncludent connections between ideas. Drawing conclusions
based on causal argueing fits perfectly to work in mathematics or to do
commercial book-keeping. Often, we overlook that this way of thinking is
not the only way possible. Thinking also makes use of analogies, which may
give us access to Kepler's opus. By using the excellent material he inherited
from his master Tycho de Brahe, Kepler found that the ratios of the planets'
track radii form equivalences to musical harmonies. Even more: Astrology
uses such data to find coincidences between the locations of the planets
and a man's horoscope. By this, we find Kepler on the search for hidden harmonies
and analogies between the celestial sphere and the living on earth. He
interpreted his results in the tradition of phytagoreism. Then astrology
can't be defined as a matter of its own, but as a research for the secrets
which obviously imply the presence of a planning creator. Science can uncover
a part of his plan and harmonies which for sure must have been intended.
Those who want to learn more about Kepler may want to read Konrad Haase's
Johannes Keplers Weltharmonik.
To make things clear: Analogies do not necessarily imply causalities! If
I find some time, I will return to this interesting topic.
3. Original German text: "Wenn
eine Masse von 1 Pfund von 4 Ellen herabfällt, erhält
sie eine solche »Kraft«, die sie wieder ebenso hoch hebt. Wenn
hingegen eine Masse von 4 Pfund 1 Elle herabfällt, erhält
sie eine »Kraft«, sie wieder 1 Elle hoch zu erheben. 1 Pfund
4 Ellen hoch zu heben, müsse aber auf dasselbe hinauskommen, wie
4 Pfund 1 Elle hoch zu heben.[...]" The German Elle has
been translated as yard, which is correct in linguistic terms but
gives the wrong impression of dimensions. 1 Elle in Hannover, where
Leibniz worked, is 58.4cm whereas a today's yard is 91,4cm. cf. Trapp:
Kleines Handbuch der Maße, Zahlen, Gewichte und der Zeitrechnung.
4. Original German text: "In einem abgeschlossenen
System, d.h. in einem System, dem von außen weder Energie zugeführt
noch entzogen wird, indem sich beliebige (mechanische, thermische, elektrische,
chemische) Vorgänge abspielen, bleibt die vorhandene Gesamtenergie
unverändert"
5. To be more precise, they
shall not accept these machines. But they do it, because of
whatever reasons. Actually, my archive contains more than 1400 patents for
PMMs between 1850 and 2000.
6. Original German text: "...im unteren Teil
des Ständers angebrachten Motor mit einer handgelenkten Bremse versehen,
um den Übergang der Maschine in eine dauernde Bewegung zu
verhindern"
7.
Bourbaki:
Pseudonym of a group of mathematicians who published their fundamental treatises
under this name. They published serious theoretical hardcore-math manuscripts.
So don't confuse the two Bourbakis!
| Last update: 22 May 2004 /
|
|