Translation ongoing!
Overbalanced wheels or unbalanced wheels are the oldest known type of perpetual motion machines. The first wheel of this kind was described by the indian astronomer and mathematician Brahmgupta at 624AD. His idea is the starting point of a whole set of concepts.
 |
Note well, that Brahmagupta talks in his Brahmasphutasiddhanta about a wheel with hollow spokes, but there is not hint about asymmetry! It is strange to think that a mathematician of his legendary skills did not make a critical approach to this concept, as the symmetry does not prefer any direction of rotation. Symmetry always implies reversability of processes, but maybe science 1400 years ago did not make these distinct considerations. Later concepts introduced an asymmetric arrangement of the moveable masses, which remained a major aspect of unbalanced wheels until today. |
Bhaskara was the one who described a wheel with curved and tuy asymmetric spokes around 1150. The idea was communicated by arabian mathematicians and seems to have been circulated widely in Europe until 1200. Villard de Honnecourt described his wheel with seven mallets at the circumference around 1230 and his notes give hint that the idea was already widespread.
Let's have a closer look at a typical overbalanced wheel.
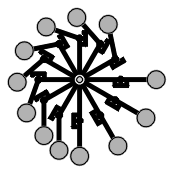
Lever-based perpetual motion machine
This device can be started into any desired direction, but it will cease running after a short while. It was expected that due to the asymmetric arrangement of masses, a permanent unbalanced torque should result. So does the law of levers not apply here? It does. The inventor has missed some important points:
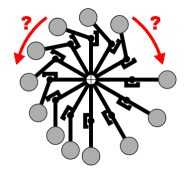 |
1. | Auf der linken Seite sind zwar die Hebel kürzer, aber die Anzahl
der Massen größer, so daß insgesamt die Momente ausgeglichen
werden können. Ich schreibe hier bewußt können, denn
es gibt viele Stellungen der Maschine, in der die Momente nicht ausgeglichen
sind. Bewegt man das Rad in eine dieser Positionen, so bewirkt das einseitige
Drehmoment, daß sich das Rad in einen Gleichgewichtszustand bewegt.
Könnten die Lagerreibung und andere Störeinflüsse ausgeschlossen
werden, würde der Mechanismus ewig oszillieren, genauso, wie er ewig
rotieren würde, wenn er mit genügend Schwung angeworfen wird. Im
Sinne der Definition ist das aber kein PM! In welche Richtung soll dieses Gerät bevorzugt laufen? Nach rechts, wegen der längeren Hebel? Oder nach links, wegen der größeren Anzahl Massen? |
|
 |
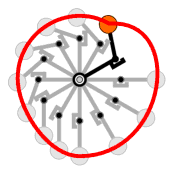
2. | Für das Drehmoment ist nicht der radiale Abstand der Masse zum Drehpunkt von Bedeutung, sondern ausschließlich der Abstand zwischen der senkrecht wirkenden Kraftlinie und dem Drehpunkt. Hier unterliegen viele Laien oft demselben Trugschluß wie der Konstrukteur dieser Fahrradtretkurbel um 1900. So ist bei senkrecht nach unten in C angreifender Kraft der wirksame Hebelarm der Abstand A-C und nicht A-B. | |
 |
3. | Der Energieerhaltungssatz gilt für die Massen in dieser Maschine.
Wenn man den Weg einer einzelnen Masse betrachtet, dann vollführt sie
einen zyklisch geschlossenen Weg. Und in seiner allgemeinen Form kann der
Energieerhaltungssatz in seiner Ausprägung als Potentialsatz so formuliert
werden: Wird ein Körper im Gravitationsfeld
auf einer geschlossenen Bahn zum Ausgangspunkt zurückbewegt, ist die
dafür aufgewendete Arbeit = 0. Anders ausgedrückt: die Arbeit, die durch die Bahn einer Masse auf der rechten Seite des Rades gewonnen wird, ist exakt die Arbeit, die notwendig ist, um dieselbe Masse wieder auf der linken Seite des Rades auf die ursprüngliche Höhe anzuheben. Die Anzahl der Arme, die Drehrichtung und die Momentangeschwindigkeit der Massen haben deshalb keinerlei Einfluß auf die (Nicht-)Funktionsweise! |
|
***image***
***image***
text
| Last update: 21 May 2004 / |
|