- input energy
- output energy
- and losses
If we want to approach the secret of perpetual motion machines, we need to have a method to analyze how they are intended to work and how they really do. Daily engineering work is based on standard construction elements, recepies and knowledge by experience. Additionally, mathematical or computer-based methods are used to predict the behaviour of a construction. If we accept PMM inventors as engineers like all others, who present their construction to the public, we also should apply the same methods which are widely used in engineering and physics. At this point, we need to clarify that we regard machine elements as they are; if e.g. a belt drive inside a construction is used, we know particular properties of this construction element, like efficiency, sensible speed range or sizes to transport a certain amont of power. Typically, PMM invertors use these elements as necessary portions of their construction.
Sometimes, it is very convenient to reduce the whole system to be analyzed to a diagram that indicates the flows of energy and the moved media. Thus we can concentrate on the analysis without being influenced by technical details.
As this chapter argues in engineering terms, we are allowed to use the expression
"loss" for all energy which runs through our system but cannot be transformed
to useful work. In physics, this energy is no loss at all, as it simply is
transformed e.g. into heat which warms up the construction. Parts of these
"losses" can be re-used. If you drive a car, the engine heats up, which makes
a cooler necessary. In engineering terms, this is lost energy. However, we
can attach a heat exchanger to the cooler and recycle part of this loss for
the heating and ventilation system.
This consideration should also make clear, that an analysis of a technical
system always requires a definition of its boundaries in order to identify
the energy flows.
Reproduceability of results is an extremely important point which me must be aware of. If we can't assume that same conditions of simple causal systems produce same results, all further discussion is without sense. Of course there are mechanical systems which show chaotic behaviour, but we shall exclude them from our considerations as they may not provide the intended reproduceability of perpetual motion behaviour of a particular machine design. If so, we can at least assume that a certain amount of energy (without knowing exactly what energy is) that will run into a particular machine should cause the same effect. We all know that machines usually have losses which is the reason for PMM inventors to overcome the energy problems. Let's analyze how energy flow in machinery works!
 |
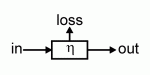
A mechanical element can be regarded as black box (computer
scientists will love this) with an efficiency of
h. If we assume that the element does not contain
hidden energy sources like batteries or fuel, we can reduce the analysis
to three energy flows:
|
Depending from the efficiency h of the mechanical element, the losses may be zero or it may consume all input energy, e.g. if the system is a vehicle brake - or something in between. We should not assume an h > 1 now, as this would imply that a singular mechanical element can generate energy out of nothing. According to the abovementioned definition, we know that h is:
In practical applications, h = 100% will not be reached, as according to today's knowledge, even very effective machine elements will have some losses. It should be clear that our black box can be very simple or arbritraily complex. Be definition, we know:
Primitive machine elements are no useful machines. Thus, the next step is to analyze the energetic implications of machine elements which are combined to systems. Basically, we need to consider the distribution of energy to several elements and the chaining of elements. Arbitrarily complex systems can be constructed by recursively applying the two principles shown here.
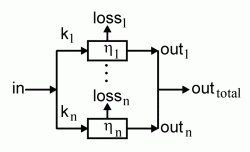 |
Assume, the system consists of n mechanical elements to which the input
energy is distributed. n might be two or more. Distribution means, the whole
input energy flow is split into several paths and each path i gets a fraction
ki, where the sum of all partials k1 to kn
is exactly 1. So we assume
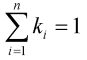
|
There might be the argument, that the total could be greater than 1, but this would require that a construction of two elementary machine elements (i.e. black boxes) is possible which have a total k1 + k2 > 1. At this point we could stop further research, since we already have found the PMM.
The total efficiency h of the system with distributed energy thus calculates to the sum of the paths' efficiencies:
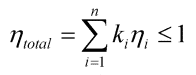
Mathematicians will have few difficulties to see why the total is not more than 1. Those who want a more obvious demonstration should look at the next diagram. One axis represents the total energy, split into fractions k1 to kn. The other axis represents the efficiencies h1 to hn.
 |
The total energy fed into the system is the input energy applied with an efficiency of 100%. The sum of the resulting partial efficiencies ki.hi is represented by rectangles of appropriate size. Can these sum up to more than the size of the enclosing square? |
The second important principle to analyze the energy flow inside a system is the chaining of (mechanical) elements. Here, we calculate the total efficiency of a system which contains n chained elements, n ³ 2:
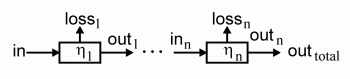 |
The first machine element will work with efficiency h1. Thus, the output energy delivered to the next element is less or equal to the input energy of the first element. The total energy that is delivered to the output of n stages of this type can be calculated by the product of efficiencies hi of the single elements. |

Easily can bee seen that a product of factors less or equal to one will result in a value less or equal to one. Again, we illustrate this result by using a diagram of efficiencies:
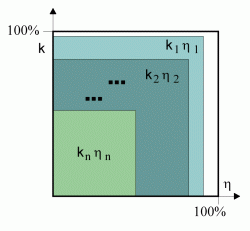 |
Every stage in the chained system will cut out a corner of the total product energy by kihi. If you always cut away parts of a fraction of a fraction..., will this grow to more than the original piece? You can't nibble away pieces of the cake and keep it! |
It should be clear that this analysis is not restricted to classical mechanical elements, but that the results will also hold for electric circuits or magnetic devices or mixed systems. In theory and practice, frequently machines are not so simple. Especially the case of thermodynamic engines, like steam engines or combustion motors require mathematical skills and methods beyond the intended scope of these pages. In analysing systems, care has to be taken to restrict the analyzed system to the appropriate portion. Often, wrong assumptions of the boundaries of a system led to misinterpretations of energetic behaviour of constructions which were regarded as PMMs.
The diagrams above indicate the distribution of energy between several black boxes. Up to now, we did neither analyze nor define the term "system". It is crucial to a particular construction that we are aware of its boundaries. Let's define:
| Definition: | System | |
|---|---|---|
|
|
|
|
| Remarks: | In | |
As a by-product of our definition and analysis, we should notice the fact that energy can be distributed or energy flows can be added. Formally, we indicate this by nodes. A four-cylinder piston engine is a good example for the mechanical addition of energy:
PMM inventors or persons who constructed "overunity" machines state that
in general terms their construction delivers more energy than fed into it.
We can regard the case of a construction that needs no input energy at all
as a special case of the general case. However, we need to be careful about
the term efficiency h, as it cannot be applied
in this case (if zero is multiplied with whatever term, the result is
zero).
It is useful to make clear what this means. Let's have a look at the first
diagram again!
 |
If an efficiency h > 1 is assumed, we still need to talk about losses. In this special case, they would be negative. If we do not want to think in negative figures, it is best to revert the arrow, now pointing to the black box. |
| Here we clearly indicate that an energy flow runs into the black box, and everything formally is ok. |
Diagrams which are formally correct do not imply feasability in terms of technology. The question, from which the energy flow runnig into the whole system originates, remains unanswered.
Feedback is a major principle in engineering, as it allows control of machines or amplification of weak signals with a minimum of technical effort. It is no surprise that perpetual motion machines use to utilize an internal feedback mechanism that is intended to amplify the internally generated energy or the energy exernally provided. A closed loop can cause confusion, as it might be unclear how the feedback influences the rest of the system. If we want to analyze the performance of a closed loop system, we just cut the system at an appropriate place and analyze the "stretched" system!
yyy
***image***
Engineers and inventors of PMMs frequently and familiarily use these results to make calculations to clarify the workability of their machines. We find standard machine elements, say mechanical or electrical, in PMM machines. Most inventors freely use widely adapted construction schemes for their machines. This is legitimate, as it gives a solid basis for engineering development. However, as soon as their construction is intended to be over-unity, they ignore the principles they have used to enclose the "magic portion" of their device and claim that this does not hold for their contraption. This directly leads to the final considerations I have made for this physics section.
I'd like to point out, that in this analysis the law of conservation of energy or other basic laws have not been used. However, we potentially could finish the whole discussion of perpetual motion machines here, as we just have demonstrated the first and second law of thermodynamics with elementary methods. Keep in mind: you can't win, you even can't break even! However, analyzing would-be PMMs is great fun and provides useful insights into the history of science and technology - and of course is a good pastime to learn more about ingenious and not so ingenious inventions.
| Last update: 22 May 2004 / |
|